Tag: mathematics
-
Limit theorems explained
Before we dive into the theorems let’s tackle a concept one often sees in statistics: the notion of independent, identically distributed (iid) random variables. Whether we’re drawing a sample from a population or conducting a series of experiments like coin flips, we can assess whether iid holds true or not as follows: Independent? Here we…
-
Calculus rules to live by
Calculus is a big topic, but by and large, there are quite specific aspects of calculus that come into machine learning and in particular deep learning algorithms. This article is not intended to explain how and why things are as they are; rather it’s my own personal cheat sheet for when I need to remember…
-
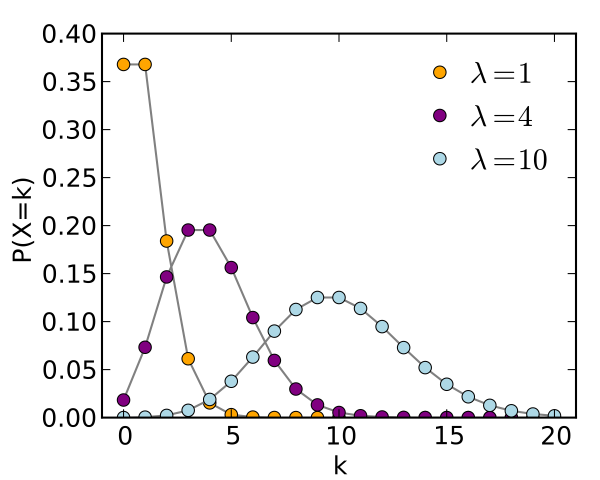
Poisson vs Exponential distributions
These distributions are related yet different – here’s a comparison that hopefully clears up any confusions! Poisson Exponential Number of events that occur in an interval of time Time taken between 2 events occurring For example… the number of Metrorail trains that arrive at the platform in an hour For example… the time between one…
-
Law of total probability – worked examples
According to Wikipedia the law of total probability “expresses the total probability of an outcome which can be realized via several distinct events”. We can also think of this as the marginal probability: irrespsective of what road we took to get to this outcome, what is the total likelihood of the outcome occurring? Example 1…
-
Expected value refresher
The expected value of an event is its most likely outcome. Assign each potential result a probability. The expected value is sum of all the potential results x their respective probabilities: ∑ (potential_result1 x probability1,… potential_resultn x probabilityn) Consider the simplest example possible, the coin flip. You’ll be paid R10 if you pick tails, but…
-
Polynomial regression
Polynomial regression is a considered a special case of linear regression where higher order powers (x2, x3, etc.) of an independent variable are included. It’s appropriate where your data may best be fitted to some sort of curve rather than a simple straight line. The polynomial module of numpy is easily used to explore fitting the best…
-
Co-variance, Correlation & Linear Regression
Typically we have 2 sets of values and we want to find out if these 2 sets of values are related, and if so how, and by how much? Could height be indicative of weight? Could hours of practice be related to how many errors are made in a mathematical test paper? Co-variance is a…
-
Linear algebra – check!
It’s been a quiet few weeks on this blog as I spent nearly every spare moment wrestling with the challenges of linear algebra – and I’m in a celebratory mood this afternoon having passed everything within time! I must say that, having some tentative foundational skills, I’m left with 2 main feelings: A tremendous sense of…
-
A gem of a book :)
I’ve just bought this delightfully titled book: No bullshit guide to linear algebra by Ivan Savov. It’s not necessarily easy learning everything you need to know about linear algebra for machine learning in 5 weeks (is that just me???) – so when I hit a bit of a brick wall in week 4 I went looking…
-
Conditional probability refresher
Probability is always… A number between 1 (certain) and 0 (impossible): The probability experiment This is process that can be repeated and in which the outcome will be uncertain, for example rolling a dice, tossing a coin, or selecting a card from a pack. The sample space This is the set of all possible outcomes…
Sho't left to data science 